Leonhard Euler 1707 yılında doğmuş ve 1783 yılında ölmüştür. Kendisinin bulduğu meşhur -e- sayısı soyadının ilk harfi ile sembolize edilmiş ve 2.71828 değerinde bir sayıdır. Bu sayı logaritma ve üstel sayıların ifade ve çözümünde kullanılıyor. e sayısı artış fonksiyonlarının ve büyüme fonksiyonlarının temelini oluşturuyor. Bu sayı çan eğrisi hesaplamalarında kullanılıyor. Tekrarlanan deneylerin başarı oranlarını hesaplamak için yine e sayısı kullanılıyor. Mühendislik bilimlerinde en temel sayı olarak euler sayısı kullanılıyor.

Euler Kimdir?
Euler matematiği fizik ve astronomi dalını yakından ilgilendiriyor. Bu dahi 64 yaşına kadar matematikle ilgilendi, 64 yaşında kör oldu. Kör olduktan sonra da Euler matematikle daha fazla ilgilendi. Gözleri dış dünyadan gelen verilere kapalı olduğu için tek penceresi sonsuz zihni oldu. Bu zihni ile matematiğin, tavşan deliklerine sızmayı başardı. Aslında kör olduktan sonra daha verimli çalıştığını söylemek yanlış olmaz.
1707 yılında İsviçre’de doğan Leonhard Euler, 4 çocuklu ailenin en büyük evladıydı. Babası hem papazdı hem de Bernoulli ailesinin yakın dostu olarak fizik ve matematikle özel olarak ilgileniyordu. Oğlunun zihinsel matematik becerisi gördüğünde onu bu alana sevk etmek istedi.
Euler’in Hayatı ve Eserleri
Euler 13 yaşında Basel üniversitesine kayıt oldu 3 yılda bu üniversitenin felsefe bölümünü bitirdi. Euler piyasada yokken Bernoulli ailesi matematik alanında otorite sahibiydi. Bu yüzden Bernoulli, Euler’e 3 yıl özel matematik dersi verdi. Euler Basel üniversitesinde profesör olmak istedi ancak bu isteği gerçekleşmedi. Daniel Bernoulli’nin desteği ile Rusya’daki bir üniversitede ilerledi. Burada da ilgisiz bir alan olan coğrafya bölümünün başına geçti. Euler’i yıldız yapan şey, basel problemini çözmesiydi.
Euler mechanica isimli bir kitap yazdı. Daha sonra fizikte hareket yasaları üzerine araştırmalar yaptı. Açısal momentum ve doğrusal momentum temellerini bu adam atmıştır. Katı cisimler için diferansiyel denklemleri yazdı. 1748 yılında sonsuzluk analizine giriş isimli kitabı yayınladı. Sonsuz serilerle matematik fonksiyonları üzerinde çalıştı. 1755 yılında diferansiyel analizin temellerini attı. Karekök içinde -1 ifadesini “i” olarak sembolize edip formülünde kullandı. Üstel fonksiyonları, trigonometrik fonksiyonlarla ifade etti.
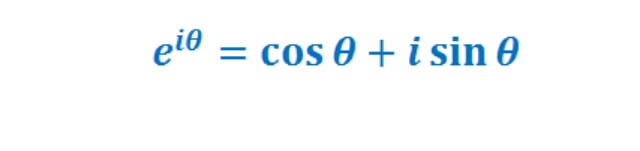








![AnTuTu testleri üzerinden en güçlü Android telefon modelleri açıklandı [Ağustos 2025] 69 d71c6d5a05fc9a2495c975cbe7e1ad67 Y29tcHJlc3NfZm9ybWF0X2pwZw 660x371 1](https://www.teknoekip.com/wp-content/uploads/2025/09/d71c6d5a05fc9a2495c975cbe7e1ad67_Y29tcHJlc3NfZm9ybWF0X2pwZw-660x371-1-280x210.jpg)












Yorum bırakın